Follow us on LinkedIn
In a previous post, we presented a methodology for pricing European options using a closed-form formula. In this installment, we price these options using a numerical method. Specifically, we will use Monte Carlo simulation.
Recall that,
- A call option gives the buyer the right, but not the obligation to buy an agreed quantity of the underlying from the seller at a future time for a given price. The payoff of the call option at expiration is max(ST-K,0),
- A put option gives the buyer the right, but not the obligation to sell an agreed quantity of the underlying to the seller at a future time for a given price. The payoff of the put option at expiration is max(K -ST,0),
where ST denotes the stock price at expiration and K is the strike price.
To price these options, we first simulate the price paths using the following Stochastic Differential Equation:
![]() where
where
- St is the stock price at time t,
- σ denotes the stock volatility,
- µ is the drift which equals the risk-free rate, and
- dWt represents the standard normal random variable.
The simulation is carried out until the options’ maturity. We then apply the terminal payoff functions and calculate the mean values of all the payoffs. Finally, we discount the mean values to the present and thus obtain the option values. For a more detailed presentation of the Monte Carlo method, see Reference [1].
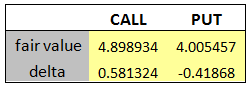
The picture below shows the call and put option prices using 100000 simulations. All other parameters are the same as in the previous post.
![]()
We compare the above results to the ones obtained by using a third-party software and notice that they are in good agreement.
In the next installment, we will present a methodology for pricing American options using Monte Carlo simulation.
References
[1] Glasserman, Paul; Monte Carlo Methods in Financial Engineering, Springer; 2003
Further questions
What's your question? Ask it in the discussion forum
Have an answer to the questions below? Post it here or in the forum





The state of Vermont did not provide adequate oversight to prevent the massive fraud that occurred in ski area and other development projects funded by foreign investors’ money through a special visa program, a state audit has found. The financial scandal first revealed in 2016,…
Terrific work!