Follow us on LinkedIn
In the previous post, we introduced the Garman-Klass volatility estimator that takes into account the high, low, open, and closing prices of a stock. In this installment, we present an extension of the Garman-Klass volatility estimator that also takes into consideration overnight jumps.
Garman-Klass-Yang-Zhang (GKYZ) volatility estimator consists of using the returns of open, high, low, and closing prices in its calculation. It also uses the previous day’s closing price. It is calculated as follows,
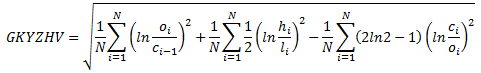
where hi denotes the daily high price, li is the daily low price, ci is the daily closing price and oi is the daily opening price of the stock at day i.
We implemented the above equation in Python. We downloaded SPY data from Yahoo finance and calculated the GKYZ historical volatility using the Python program. The picture below shows the GKYZ historical volatility of SPY from March 2015 to March 2020.
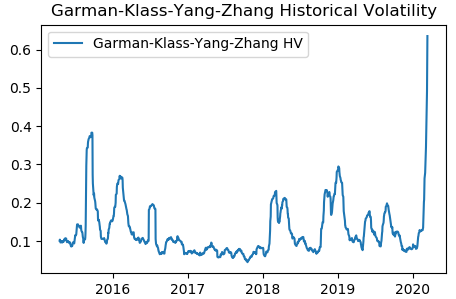
We note that the GKYZ volatility estimator takes into account overnight jumps but not the trend, i.e. it assumes that the underlying asset follows a GBM process with zero drift. Therefore the GKYZ volatility estimator tends to overestimate the volatility when the drift is different from zero. However, for a GBM process, this estimator is eight times more efficient than the close-to-close volatility estimator.
Also check out Historical Volatility Online Calculator.
Further questions
What's your question? Ask it in the discussion forum
Have an answer to the questions below? Post it here or in the forum





The state of Vermont did not provide adequate oversight to prevent the massive fraud that occurred in ski area and other development projects funded by foreign investors’ money through a special visa program, a state audit has found. The financial scandal first revealed in 2016,…
Bug in the formula – Python code
gkyzhv = np.sqrt(252 / 22 *
pd.DataFrame.rolling(np.log(spy.loc[:, ‘Open’] / spy.loc[:, ‘Close’].shift(1)) ** 2 +
0.5 * np.log(spy.loc[:, ‘High’] / spy.loc[:, ‘Low’]) ** 2 –
(2 * np.log(2) – 1) *
np.log(spy.loc[:, ‘Close’] / spy.loc[:, ‘Open’]) ** 2,
window=22).sum())
in the formula, first two terms are divided by 2. However, in the python implementation, first term is not divided by 2. Only second term is multiplied by 0.5.
Thank you for pointing this out. The error is actually in the formula. I corrected
Hi, i don´t understan why you use 252 in the numerator of the formula. Could you explain me how you obtain it value please? thank you!
252 is the number of business days in a year. Volatility scales as square root of time, so use sqrt(252) to annualize the volatility
Is it a 20 trading day lookback or 22 day?
22 days lookback
Hello. How to look at code if i don’t use facebook or twitter? Possible?
Then share this post on a social network of your choice, then send me an email.