Follow us on LinkedIn
Harry M. Markowitz is the founder of Modern Portfolio Theory (MPT) which originated from his 1952 essay on portfolio selection. He was later awarded a Nobel Prize in Economics. His work founded the concept of an efficient frontier, and it allows for the determination of portfolio mixes that provide an optimal return for the least amount of risk.
Modern portfolio theory (MPT), or mean-variance analysis, is a mathematical framework for assembling a portfolio of assets such that the expected return is maximized for a given level of risk. It is a formalization and extension of diversification in investing, the idea that owning different kinds of financial assets is less risky than owning only one type. Its key insight is that an asset’s risk and return should not be assessed by itself, but by how it contributes to a portfolio’s overall risk and return. It uses the variance of asset prices as a proxy for risk. Read more
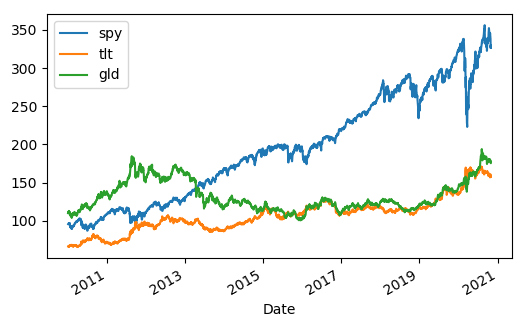
In this post, we are going to provide a concrete example of implementing MPT in Python. Our portfolio consists of 3 Exchange Traded Funds (ETF): SPY, TLT, and GLD which track the S&P500, long-term Treasury bond, and gold respectively. We downloaded 10 years of data from Yahoo Finance. The picture below shows the price time series of the 3 ETFs.
We utilized Python to calculate each EFT expected return and volatility. We then assigned a random weight to each ETF and determined the portfolio’s expected return and volatility. Recall that,
MPT assumes that investors are risk averse, meaning that given two portfolios that offer the same expected return, investors will prefer the less risky one. Thus, an investor will take on increased risk only if compensated by higher expected returns. Conversely, an investor who wants higher expected returns must accept more risk. The exact trade-off will not be the same for all investors. Different investors will evaluate the trade-off differently based on individual risk aversion characteristics. The implication is that a rational investor will not invest in a portfolio if a second portfolio exists with a more favorable risk-expected return profile – i.e., if for that level of risk an alternative portfolio exists that has better expected returns.
Under the model:
- Portfolio return is the proportion-weighted combination of the constituent assets’ returns.
- Portfolio volatility is a function of the correlations ρij of the component assets, for all asset pairs (i, j).
We repeated the above process many times and obtained the following return/risk profile for possible portfolios.
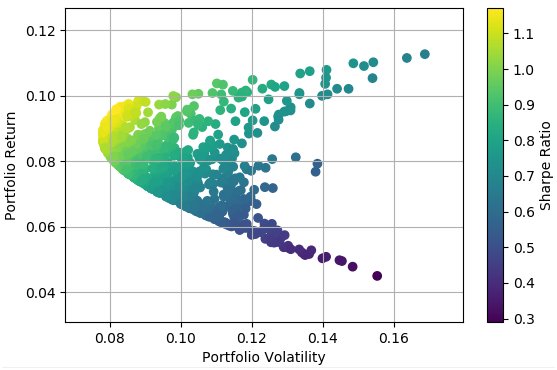
In the next installment, we will search for an optimal portfolio that provides the highest return for the least amount of risk.
Further questions
What's your question? Ask it in the discussion forum
Have an answer to the questions below? Post it here or in the forum




