Follow us on LinkedIn
In a previous post, we discussed how the dynamics of assets are priced in the options prices. We recently came across a newly published article [1] that explored the same topic but from a different perspective that does not involve options.
The conclusion of the new article [1] is consistent with the previous one [2]; that is, the volatilities of mean-reverting assets are smaller than those of assets that follow the GBM process. The reverse applies to trending assets.
In this post, we are going to investigate whether the mean-reverting/trending property of an asset has any impact on a trading strategy’s PnL volatility.
To do this, we first generate asset prices using Monte Carlo simulations. We evolve the asset prices in both mean-reverting and trending regimes for 500 days. We then apply a simple trading system to the simulated asset prices. The trading system is as follows,
Go LONG when the Relative Strength Index <40, SHORT when the Relative Strength Index >70
The picture below shows the Autocorrelation Functions (ACF) of the asset returns. Panels (a) and (b) present ACFs of the trending and mean-reverting assets respectively. It’s clear that the assets are trending and mean-reverting at lag 3, respectively.
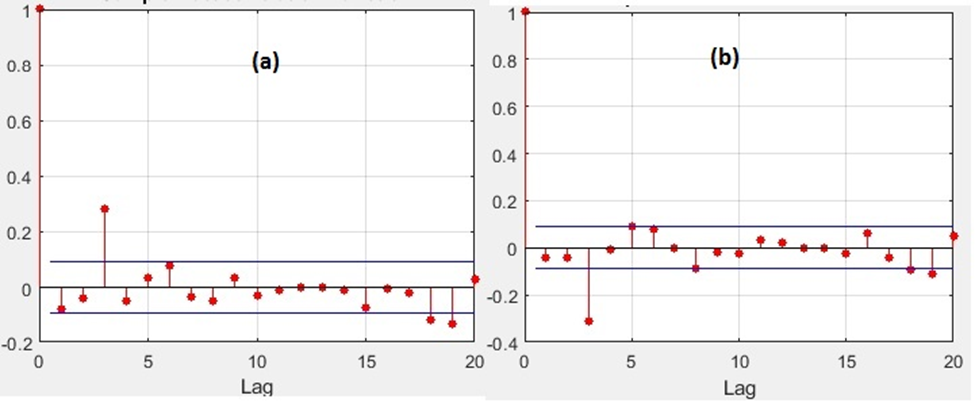
Autocorrelation Functions of asset returns
The picture below shows the simulated equity curves of the trading strategy applied to the trending (a) and mean-reverting (b) assets. The starting capital is $100 in both cases.
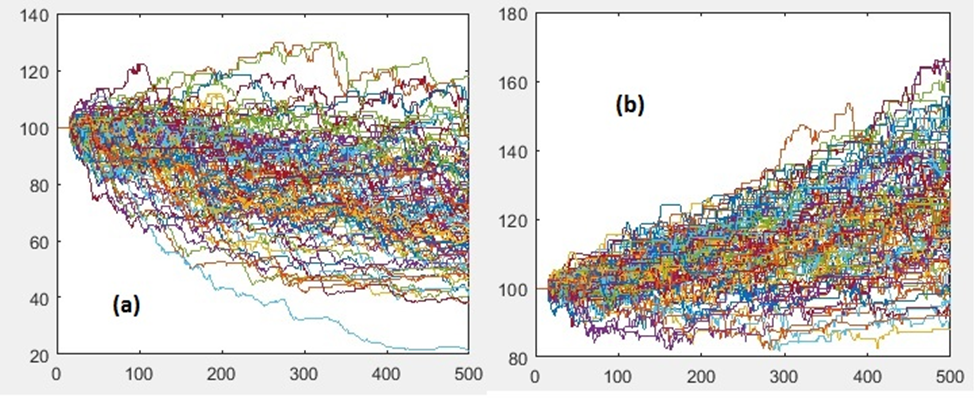
Equity curves of the trading strategy
Visually, we do not observe any difference in terms of PnL dispersion. Indeed, the standard deviation of the terminal wealth at day 500 is $18.9 in the case of the trending asset (a), and $17.3 in the case of the mean-reverting asset (b). Is the difference statistically significant? We don’t think so.
This numerical experiment shows that the PnL volatility of a trading strategy has little to do with the underlying asset’ mean-reverting/trending property. Maybe it depends more on the strategy itself? (Note that in this example, we utilize a mean-reverting strategy). What would happen at the portfolio level?
References
[1] L. Middleton, J. Dodd, S. Rijavec, Trading styles and long-run variance of asset prices, 2021, arXiv:2109.08242
[2] Liao, S.L. and Chen, C.C. (2006), The valuation of European options when asset returns are autocorrelated, Journal of Futures Markets, 26, 85-102.
Originally published on Relative Value Arbitrage
Further questions
What's your question? Ask it in the discussion forum
Have an answer to the questions below? Post it here or in the forum




